西湖论剑2021 密码学wp

unknown_dsa

前面是Pell方程，已知wl其实就是知道pell方程中的D，并且都不是平方数，因此可以通过这些根号D的连分数展开求u和v，广播攻击求m1和m2。encrypt函数里s1s2相减可以求出来k，进而求出x1，x2等，求得flag。

t就是g的phi-1次方，因此t的逆元就是g。而pq(p-1)//q=p*(p-1)，可以分解pq

解pell方程：

res = []
wl = [3912956711, 4013184893, 3260747771]
for w in wl:
    cf = continued_fraction_list(sqrt(w), partial_convergents = True, nterms = 1000)[1]
    for x, y in cf:
        if x ** 2 - w * y ** 2 == 1:
            res.append((x, y))

ul = [each[0] for each in res]
vl = [each[1] for each in res]

decrypt

from Crypto.Util.number import *
from Crypto.Hash import SHA
m1 = 8382905590662478666595114136929713707132131361720892331048437274828529226704174
m2 = 10336852405630488944198347577475266693234960398137850045398990629116544863921454
m1 = long_to_bytes(m1)
m2 = long_to_bytes(m2)
hm1 = bytes_to_long(SHA.new(m1).digest())
hm2 = bytes_to_long(SHA.new(m2).digest())

p = 95139353880772104939870618145448234251031105153406565833029787299040378395002190438381537974853777890692924407167823818980082672873538133127131356810153012924025270883966172420658777903337576027105954119811495411149092960422055445121097259802686960288258399754185484307350305454788837702363971523085335074839
q = 895513916279543445314258868563331268261201605181
g = 13672490591171261930826729213489159146697563374509073034220721886255982152303447107197774720664438144279163383740258238065494126227608731057119338486910291529176576096612311734285061607284964658737003594964324046804258074712614189778906098614765392123515385260406254416427321997510822217750260108595410657401

r1 = 498841194617327650445431051685964174399227739376
s1 = 376599166921876118994132185660203151983500670896
s2 = 187705159843973102963593151204361139335048329243
r2 = 620827881415493136309071302986914844220776856282
s3 = 674735360250004315267988424435741132047607535029

k = (hm1 - hm2) * inverse(s1 - s2, q) % q

x1 = (s2 - inverse(k, q) * hm2) * inverse(r1, q) * k % q

x2 = ((s3 * k) - hm1) * inverse(r2, q) % q
print(long_to_bytes(x1), long_to_bytes(x2))

FilterRandom

每次有90%概率从l1里面选数据，那么出现连续64个l1的数据的概率是0.9^64=0.001179，题目给了2048个数据，因此有理由相信里面有连续的64个l1的数据，那么就需要跑一下：

from tqdm import trange

N = 64

class lfsr():
    def __init__(self, init, mask, length):
        self.init = init
        self.mask = mask
        self.lengthmask = 2**length-1

    def next(self):
        nextdata = (self.init << 1) & self.lengthmask 
        i = self.init & self.mask & self.lengthmask 
        output = 0
        while i != 0:
            output ^= (i & 1)
            i = i >> 1
        nextdata ^= output
        self.init = nextdata
        return output

def backtrace(state, mask):
    _mask = ((mask & 0x7FFFFFFFFFFFFFFF) << 1) | 1
    i = state & _mask
    output = 0
    while i != 0:
        output ^= (i & 1)
        i = i >> 1

    return (output << 63) + (state >> 1)

def compare(s1, s2):
    cnt = 0
    while s1 != 0 and s2 != 0:
        if (s1 & 1) == (s2 & 1):
            cnt += 1
        s1 >>= 1
        s2 >>= 1

    return cnt / N

out = "10001011010100011000100101001011100010110111001100001110000111011011100101101101000111101100010111100011000011111111010101111100101010101100010100000111011010011110111000100000101100101010110100111100011000101010101011011111011011000001101001011000010000011110001111001111011100110011111111101000111101001010000110001110111101001001101011101101001010001101010010110000000000001001101100101011110011010110011010110110011001001111001010100011110111100100010110111100110010000000010010011110001100000011000001110001000000010000100100101100000011100000011110101001011010011010100001101000010100100000011001011001000110000000000111011101000110010110111110010101110010001010001111111000011010000011001110111001000010011000000111010111100000100010011001111101110110100100011111000111000011111101010010110011111100010000100101011000001010101111101111001000011101111000111000101011010111100110001011011100101001010110110110110011100100111100110001101110010100010111100000110000010110100010001100011011001100100110101110010100011101110110010000010011100000011100000101010011011111110000100000010001010111011011111110100111100011100011110110010001011101111001011101010110111001001000111001001111001111110111111100001111100100110011111110110101000011010111110010001100000111100010011100011010000101010111010101101000011001110011000000110110110001101100110101110010010111011100110101000110000011001010100000110000000001110010001010001001101111100001111111011010010011100110010000111010001001111111110000010101110011010100100101101100111000010110100110010001010110111110011000111011101110100010000110110110011001011111011111000000000000001110000001000011000110111000000110100110110001111011111100010010011100101010000111000011111010000001010010011101010010110011000000001111110000000010111011000010001111000100110101110001000011111001101111111100011111011001001110000101001101110100111010011011101000110010000001001000001100110001110101100001000110100100010111101100010100110011111010011100100001101111010000110110101111111001111011100001101100000001101111100100"
mask1 = 17638491756192425134
mask2 = 14623996511862197922


result = []

for i in trange(2048-N):
    this = out[i:i+N]
    l1=lfsr(int(this, 2),mask1,N)
    cnt = 0    
    for j in range(i+N, 2048):
        if l1.next() == int(out[j]):
            cnt += 1
    tot = 2048 - N - i
    result.append((i, cnt / tot))


result.sort(key = lambda elem: elem[1], reverse = True)

result2 = []
for i, each in result:
    if each > 0.8:
        result2.append((i, each))

result2.sort(key = lambda elem: elem[0])
print(result2)

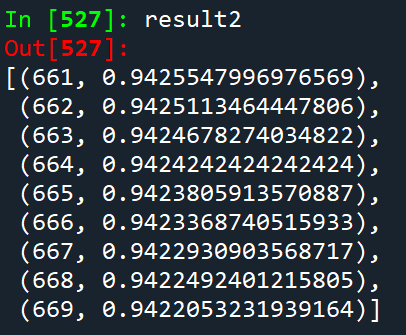
下标661处往后64个数据大概率都是来自于l1，选择之后进行backtrace回溯，就可以拿到init1

对于init2，out里不符合init1输出的都是init2，输出之后有112比特：

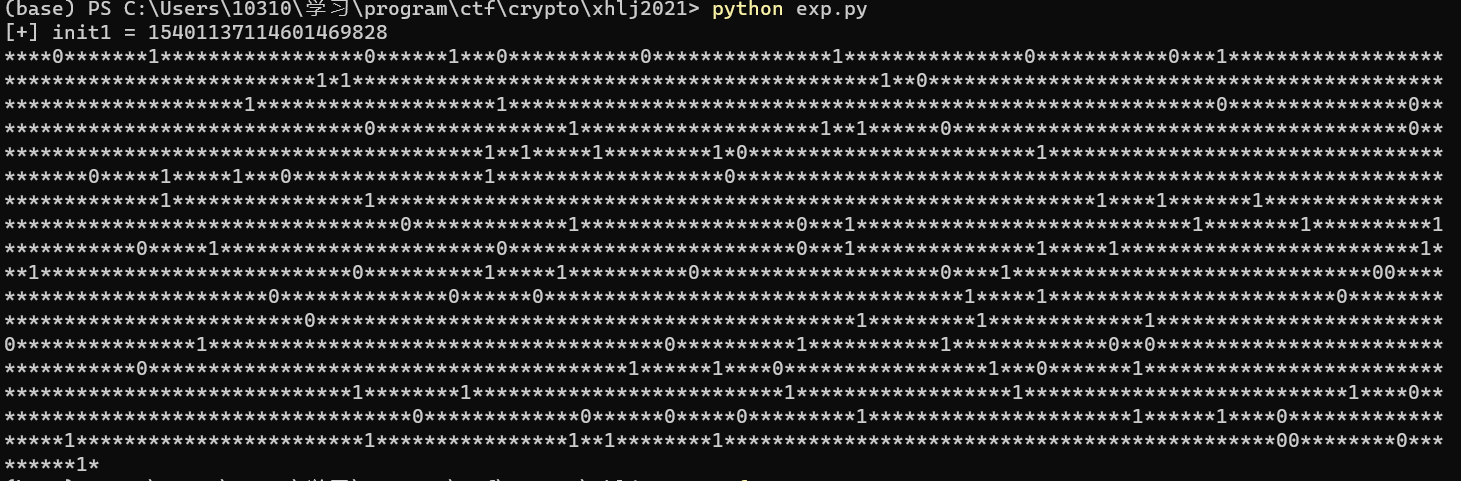
其实可以得到这样的方程：

这样就能列一个矩阵方程解。

s = "****1*******0*****************1******0***1***********1***************0***************1***********1***0********************************************0*0********************************************0**1***************************************************************0********************0***********************************************************1***************1********************************1****************0********************0**0******1**************************************1******************************************0**0*****0*********0*1************************0****************************************1*****0*****0***1****************0*******************1************************************************************************0****************0************************************************************0****0*******0************************************************1*************0******************1***0****************************0********0**********0***********1*****0***********************1************************1***0***************0*****0*************************0***0**************************1**********0*****0**********1********************1****0******************************11**************************1**************1******1***********************************0*****0************************1*********************************1*********************************************0*********0*************0************************1***************0**************************************1**********0***********0*************1**1***********************************1****************************************0******0****1*****************0***1*******0******************************************************0********0**************************0******************0***************************0****1************************************1*************1******1*****1*********0**********************0******0****1******************0************************0****************0**0********0**********************************************11********1*********0*"

ans = []

for i, each in enumerate(s):
    if each == '*':
        continue
    ans.append((i, each))


A = []
for i, each in ans:
    A.append((M ^ i * mask).list())

A = Matrix(Zmod(2), A).T
y = [each[1] for each in ans]
y = vector(Zmod(2), y)

print(A.solve_left(y))

上文中M就是LFSR的递推矩阵，因为题目是在shell做的，没保留完整exp，因此上面没写M的生成。

hardrsa

discrete_log+sage的solve就能算出来p，拿p^4算就行了。

密码人集合

数独题 就把“西湖论剑我要拿第一”映射为123456789，用sage的sudoku解就行了